In recent years, the types of man-made porous metal materials have been increasing, and they have been widely used in many fields such as aerospace, construction, medical and health. Taking the aviation field as an example, many structural parts require special mechanical properties while also satisfying the need to absorb impact energy, To provide heat dissipation and other functions, porous aluminum and other materials have been widely used. For example, the lattice sandwich panel structure has been used as a buffer and energy-absorbing component in aerospace vehicles.
At present, the preparation methods of lattice materials are laser3D printing, Weaving and casting methods.Among them, the laser3D printingAs a result, the dependence on laser printing parameters is relatively high, printing defects are prone to occur, and the casting method has mature technology and simple operation.
In order to better clarify the stress-strain behavior of the bending-dominant pyramid-shaped lattice metal and the dependence of its energy absorption characteristics on structural parameters, so as to provide a reference for further optimizing the design to meet the needs of practical applications, “Investment Casting Lattice Al The research team in the article “Mechanical Behavior and Energy Absorption Characteristics of “” uses industrial pure Al as the matrix and adopts3D printingThe method of combining technology and investment casting has prepared pyramid-shaped lattice Al with different aspect ratios and included angles (see Figure 1 for the specific process), and its compression behavior and energy absorption characteristics have been investigated. Compared with the current popular of3D printingMethod to prepare porous metal, the sample prepared by this method has fewer defects, lower cost, and a simpler preparation method.
Porous metal materials are divided into two types: open-cell materials and closed-cell materials.
The open-pored material has connectivity between the holes, and has the functions of sound absorption, heat dissipation, and filtration at the same time, which has very broad application prospects. The two more important branches of open-pored metal materials are foam metal and three-dimensional lattice metal. When deformed under force, the deformation mechanism of the former is bending-dominant. When the number of rod elements at the junction is 12, the deformation mechanism of the latter is tensile-dominant. In comparison, lattice metal has better advantages. For example, when the relative density of the material is 10%, the strength of lattice metal is 3 times that of foam metal. However, it can be seen from the stress-strain curve and deformation characteristics of the tensile-dominant lattice metal that when the yield strength is reached, the bar will yield and soften, which is not conducive to its application in energy absorption. Due to the regularly arranged pore structure of the pyramidal lattice metal dominated by bending, there is no softening phenomenon on the compressive stress-strain curve. Therefore, it is of great significance to study the bending-dominant three-dimensional lattice metal materials.
Figure 1 Schematic diagram of the experimental process of preparing lattice aluminum by casting method
1 Test process
The pyramidal lattice unit cell is composed of a four-sided pyramid top-to-top. The three-dimensional diagram is designed using CATIA V5R20 software. The main design parameters are shown in Figure 2a and Table 1. The key structural parameters of the pyramidal lattice material mainly include: the length of the rod L, the diameter D of the rod, and the angle ω between the rod unit and the bottom surface of the unit cell. As a kind of porous materials, relative density is an important factor affecting the mechanical properties of lattice materials, and its value is ρ0/ρs, where ρ0 is the apparent density of the prepared lattice material; ρs is the density of pure aluminum.
Take photosensitive resin as raw material, adopt light curing3D printingThe lattice model is prepared by technology, and then the model is used as the sacrificial mold, and the industrial pure aluminum with a mass fraction of 99.7% is used as the matrix to prepare lattice Al through the investment casting process.
The main process of the method is as follows: Place the photosensitive resin lattice material in a cast iron mold, then pour a certain proportion of gypsum slurry into the pores of the lattice material, and then go through the processes of natural drying, low-temperature drying, and high-temperature roasting. The photosensitive resin material is burned out and the gypsum is cured to obtain a gypsum mold with a lattice structure cavity. Finally, use an air compressor to hydraulically press the high-temperature aluminum into the plaster mold at a certain pressure. After the natural cooling, the aluminum liquid solidifies and obtains the lattice Al blank. The plaster mold is washed with a high-pressure water gun, and the X/Y/Z is cut by the wire cutting technology. The compressed samples with directional unit cells of 7/7/4 are shown in Figure 2c. The Instron 3369 mechanical testing machine was used for the quasi-static compression test. The compression direction was the Z-axis direction and the compression rate was 2 mm/min.
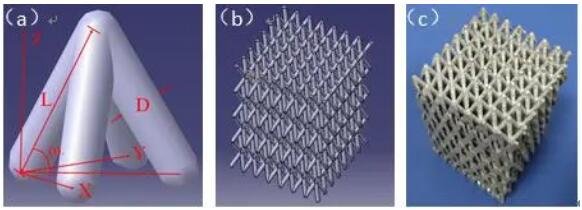Figure 2 Pyramid lattice structure and lattice Al
(A) Pyramid unit cell structure parameters;
(B) Overall structure diagram;
(C) Lattice Al
2 Results and discussion
2.1 Compressive stress-strain behavior of lattice Al
Figures 3 and 4 are the compressive stress-strain curves of lattice Al. It can be seen that, unlike the tensile dominant lattice material, the stress-strain curve does not appear to soften after the linear elastic zone, but is similar to the general bending dominant porous material, with three typical regions, namely the linear elastic zone. , Stress plateau area and densification area.
In the linear elastic zone, the lattice material rod element only undergoes elastic deformation, and the stress and strain become linear. Although its linear value is not as large as that of the stretch-dominant lattice material, it has a stronger linear relationship than the open-cell aluminum foam. This phenomenon may be due to the fact that it is a bending-dominated porous material like the open-cell aluminum foam, but has a regular arrangement of lattice materials under the stretching dominance.
The irregular arrangement of the open-cell aluminum foam causes partial buckling of part of the unit cells under lower stress. There is a smooth transition between the linear elastic region and the stress plateau region. The stress in the stress plateau region rises steadily as the strain increases, and the magnitude of the increase will vary with the structural parameters.
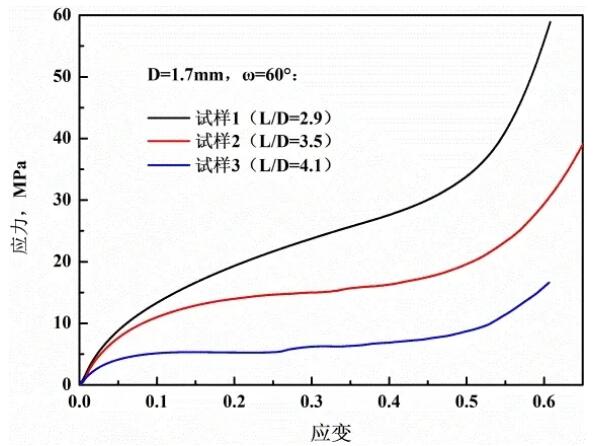Figure 3 The influence of the aspect ratio on the compressive stress-strain curve of the specimen when the included angle is 60°
It can be seen from Figure 3 that when the included angle is 60°, the aspect ratio increases, the relative density decreases, the magnitude of the stress rise in the plateau area decreases, and the flow stress decreases. This phenomenon is due to the smaller the relative density, the higher the porosity, and the local rods are not prone to pre-contact during the compression process. For the pyramid-shaped lattice material, when the included angle and the aspect ratio are the same, the flow stress is basically unchanged. In this study, the increase in the aspect ratio is to keep the rod diameter constant while increasing the rod length. When the included angle does not change, the increase in the aspect ratio is equivalent to the rod length being unchanged and the rod diameter becomes thicker, so that the specimen can withstand greater force under the same strain, so the smaller the aspect ratio is The greater the stress. It is worth noting that the flow stress and the aspect ratio are not strictly inversely proportional. When the strain is 0.3, the aspect ratio decreases from 4.1 to 3.5, and the flow stress increases from 6.2 MPa to 15 MPa. In addition, the flow stress value and the relative density are also non-linear. When the relative density increases from 0.33 to 0.51, the flow stress value rises from 6.2 MPa to 23.6 MPa. This phenomenon shows that the aspect ratio has a greater influence on the flow stress than on the relative density, so when the relative density does not change much, the aspect ratio can be appropriately reduced to obtain a larger flow stress value.
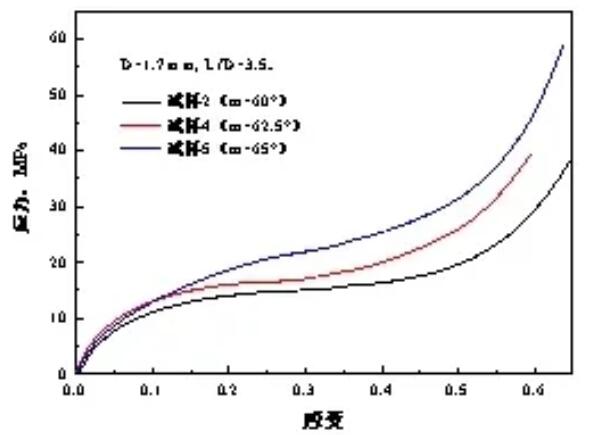Figure 4 The influence of the included angle on the compressive stress-strain curve of the specimen when the aspect ratio is 3.5
It can be seen from Figure 4 that when the aspect ratio is 3.53, the flow stress of lattice Al increases with the increase of the included angle. This is because in the case of the same sample size, the greater the angle, the greater the number of unit cells, which leads to an increase in relative density, and therefore, the greater the flow stress. It can also be seen from Table 1 that when the ratio of length to diameter is fixed and the angle is between 60° and 65°, when the angle is not greatly changed, the relative density can be changed greatly, and the flow stress value can be changed. Big change. In addition, through the force analysis, it can be seen that when the included angle increases, the component force received by the rod in the vertical direction will increase, and the component force received in the horizontal direction will decrease, so it is less likely to yield, which leads to Its flow stress is greater.
2.2 Energy absorption characteristics of Al-based lattice materials
Figures 5 and 6 show the energy absorption curves per unit volume of lattice Al. It can be seen that the energy absorption per unit volume of lattice Al increases with the increase of strain. In the linear elastic area, the energy absorption of the lattice Al is less; after entering the platform area, the energy absorption of the lattice Al increases significantly. This is because in a wider strain range, the stress value is large and the change is small; it enters the densification After the zone, the stress increases greatly. This is because the lattice Al holes are basically compacted. Although the energy absorption is still increasing, this part of the energy absorption is mainly absorbed by the dense Al matrix and does not affect the objects that need to be protected. To the protective effect.
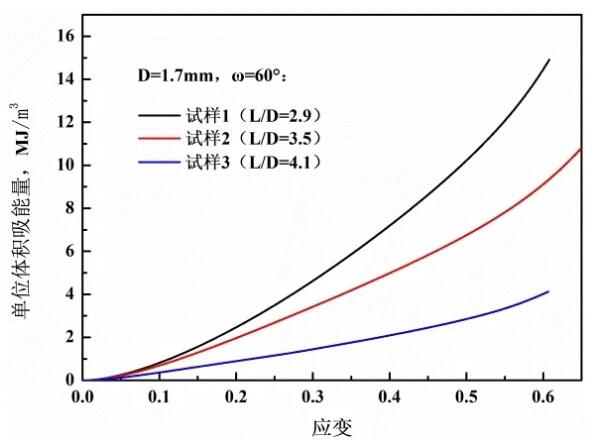Figure 5 The influence of the aspect ratio on the energy absorption curve per unit volume when the included angle is 60°
Therefore, the effective energy absorption per unit volume of lattice Al is the energy absorption per unit volume at the compact point. When the angle is 60°, as the aspect ratio increases, the absorption capacity of lattice Al gradually decreases. This is because when the strain is the same, as the aspect ratio increases, the stress of the lattice Al becomes smaller, as shown in Figure 5. When the aspect ratio is 3.53, the included angle increases, the relative density increases, and the flow stress value also increases, so the energy absorption per unit volume of lattice Al increases, as shown in Figure 6.
Figure 6 The influence of the included angle on the energy absorption curve per unit volume when the aspect ratio is 3.5
The energy absorption efficiency curves are shown in Figure 7 and Figure 8. Different from the energy absorption curve per unit volume, as the strain increases, the energy absorption efficiency first rises and then falls. In the elastic zone and the plateau zone, as the strain increases, the energy absorption efficiency gradually increases; the strain when the energy absorption efficiency reaches the maximum is the strain at the dense point. Near the densification point, the capacity absorption efficiency changes slowly and maintains a high level. This is because entering the densification area from the platform area is also a smooth curve without a very obvious densification point. After entering the densification zone, the energy absorption efficiency begins to decrease, which is caused by the stress value increasing faster than the relative capacity absorption value.
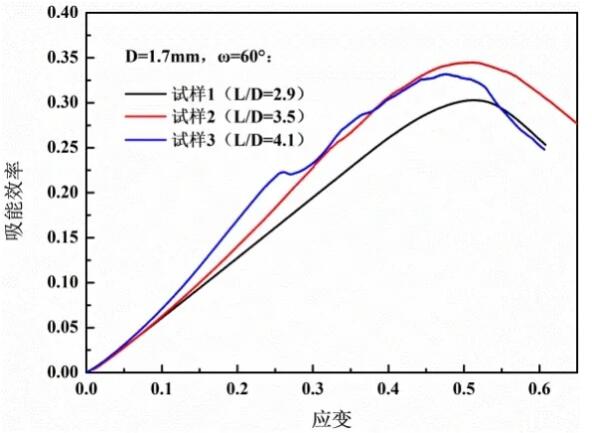Figure 7 The influence of the length-diameter ratio on the absorption efficiency curve of the sample when the included angle is 60°
It can be seen from Figure 7 that when the strain is less than 0.3, as the aspect ratio increases, the energy absorption efficiency gradually increases, but when the strain is greater than 0.45, the energy absorption efficiency is the highest when the aspect ratio is 3.5. At the same time, it is also found that the length When the diameter ratio is 2.9 and 3.5, the strain at the densification point is both 0.51, and when the aspect ratio is 4.1, the strain at the densification point is 0.48. It shows that the included angle remains unchanged, and the length of the stress platform is not directly proportional to the ratio of length to diameter. The difference is that when the aspect ratio is constant, with the increase of the included angle, the strain value of the densification point does not change much, all around 0.51, as shown in Fig. 8. The energy absorption per unit volume at the compact point is shown in Figure 9. It can be seen that by appropriately increasing the angle or reducing the aspect ratio, the energy absorption per unit volume at the compact point can be increased.
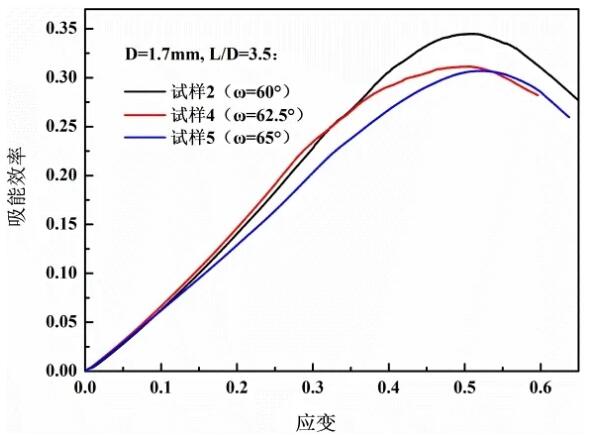Figure 8 The influence of the included angle on the absorption efficiency curve of the sample capacity when the aspect ratio is 3.5
Figure 9: Energy absorption per unit volume of the sample
3 Conclusion
(1) The stress-strain behavior of cast pyramid lattice Al is similar to ordinary foam Al, with obvious linear elastic zone, stress plateau zone and densification zone
(2) The flow stress value of lattice Al increases as the aspect ratio decreases, but it is not strictly inversely proportional. When the aspect ratio is constant, the included angle increases, the relative density increases, and the flow stress of lattice Al increases.
(3) At the point of densification, the energy absorption per unit volume of lattice Al increases with the decrease of the aspect ratio, and increases with the increase of the included angle.
(Editor in charge: admin)
0 Comments for “Mechanical behavior and energy absorption characteristics of 3D printing + investment casting pure aluminum pyramid lattice”